Stochastische Kräfte und Ferromagnetismus
(T. Bose, Prof. S. Trimper)
Physikalische Systeme können oftmals rein deterministisch beschrieben werden. Für bestimmte Vorgänge ist es jedoch notwendig auch stochastische Komponenten in die Beschreibung mit einzubeziehen. Ein prominentes Beispiel dafür ist die Brownsche Bewegung.
Die Idee ist nun schwach angeregte ferromagnetische Systeme unter dem Einfluss von stochastischen Kräften zu untersuchen. Als Ursache für ein solches Rauschen kann man sich beispielsweise fluktuierende Kopplungskonstanten aufgrund von Defektkonfigurationen im Kristall vorstellen. Als Modell dient ein idealisierter Ferromagnet, d. h. es wird eine Domäne betrachtet, die nur aus gleichartigen Atomen besteht, die alle äquivalente Gitterplätze im Kristall besetzen. In dieser Situation kann die gesamte Domäne mittels eines Makrospins repräsentiert werden. Als grundlegende Bewegungsgleichung für die Dynamik dieses Makrospins dient die Landau- Lifshitz- Gilbert Gleichung. Die Abbildung am Ende dient als grafische Veranschaulichung der entsprechenden mikroskopischen Situation.
Speziell wurde in diesem Modell die Dynamik von Spinwellen untersucht, welche den leicht angeregten Zustände im Ferromagneten entsprechen. Es sind zwei separate Dämpfungsmechanismen enthalten, einerseits ein deterministischer Anteil und andererseits eine stochastische Komponente. Jeder Mechanismus für sich dämpft die Spinwellen. Die Berechnungen haben aber gezeigt, dass eine Kompensation beider Mechanismen für bestimmte Verhältnisse kritischer Parameter möglich ist. Mit anderen Worten, die Spinwellen sind ungedämpft und der angeregte Zustand des Ferromagneten bleibt erhalten.
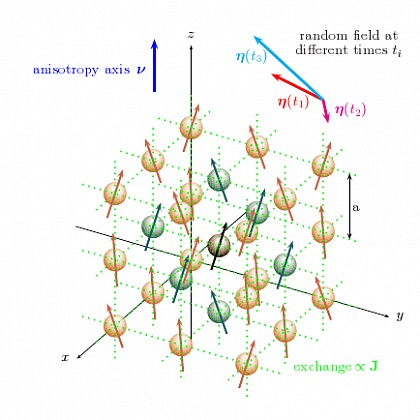
Ferromagnetische Domäne, beeinflusst von stochastischen Feldern




