Stochastic Forces and Ferromagnetism
(T. Bose, Prof. S. Trimper)
Physical systems can often be described in a pure deterministic manner. However, for some processes like the Brownian motion it is reasonable to take stochastic forces into account.
The idea now is to describe weak excited ferromagnetic systems under the influence of stochastic forces. For instance, fluctuating coupling strengths between the magnetic moments due to defect configurations in the crystal could be the origin of such a noise. In the following we consider a ferromagnetic domain in the classical limit, i.e. the magnetic order is referred to single magnetic atoms which occupy equivalent crystal positions. In this situation the system can be described by a macrospin that represents the whole domain. The basic equation of motion for this macrospin is given by the Landau- Lifshitz- Gilbert equation. The figure below serves as illustration of the corresponding microscopic picture.
In particular, the dynamic of spin waves according to the weak excited states of the ferromagnet was analyzed. The introduced model contain two separate damping mechanisms, on the one hand a deterministic one and one the other hand a random one. Every mechanism itself leads to damping. But in the situation when both act simultaneously on the system a mutual compensation can be observed for special relations of critical model parameters. In this case the spin waves will not undergo damping processes and the excited state of the ferromagnet is maintained.
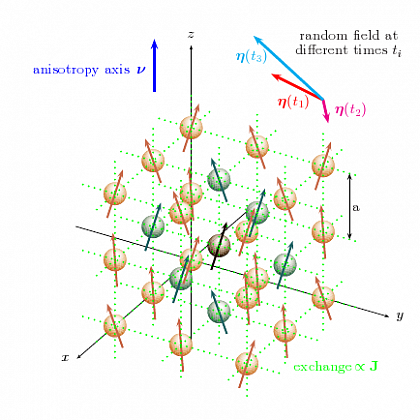
Ferromagnetic domain, influenced by stochastic fields




