Polymer Electrolytes
(A. Golovnev, Prof. S. Trimper)
The development of efficient energy storage systems is of increasing interest. Concerning electric applications such as batteries, polymer electrolytes are promising materials for ion conducting membranes separating the electrodes. Therefore, an understanding of ion transport processes in those materials is necessary.
The transport properties of polymer electrolytes are investigated. More specific, the transport of particles through the medium under the influence of applied external force is analyzed in case when both applied field and self diffusion are important. In case of polymer electrolytes subjected to a dc voltage, this phenomenon is described by the Poisson-Nernst-Planck equations (PNP) which represent the particle number conservation law supplemented by the Poisson equation. This set of equations provides a charming mathematical problem namely a number of nonlinear differential equations coupled one to another by means of an additional one. In this model symmetric binary electrolytes are considered, which turns the PNP into three coupled equations. The analysis is partly devoted to the linear regime because, even if the nonlinearity can by neglected, it is quite problematic to find the dynamical solution appropriate to boundary conditions dictated by the experimental realization.
A study of nonlinear effects is also of a great interest not only as a mathematical task but also for a description of systems where the influence of nonlinear effects is relevant such as, for example, the one shown on the picture. The exact nonlinear steady state solution for the charge concentration measured in units of the initial concentration within a thin film differs drastically from the solution of the corresponding task where the nonlinearity is omitted. The distance is measured in units of the Debye screening length λ.
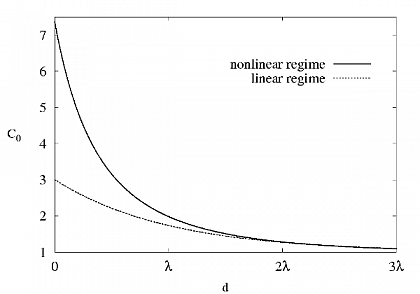
Steady state solution for the charge concentration vs. distance




