Martin-Luther-Universität Halle-Wittenberg

Kontakt

Dr. Nicki Frank Hinsche

Telefon: 0345 55 25 566
Telefax: 0345 55 25 446

Raum 0.47
von-Seckendorff-Platz 1
06120 Halle

Weiteres

Login für Redakteure

Forschungsthemen

Dr. Nicki Frank Hinsche

Dr. Nicki Frank Hinsche

The current research focus lies on the realistic description of electronic and thermal material properties of nanostructured systems beyond standard Density Functional Theory (DFT).

In detail, I am working on methods and computational implementations to understand, describe and predict electronic and vibronic transport properties in bulk and low-dimensional systems, i.e. single crystals, thin films or monolayers.

Ultimate goal is the multi-scale description of functional devices, based on phenomena like thermoelectrics, superconductivity, multiferroics, phase-change or topological insulators/metals, from the theoretical atomic scale towards the experimentally realisable material.

An overview of the publications can be found at Google scholar    and Orcid   .

Selected results of the research topics are presented below. Please click the figures for explanations and details.

2D materials

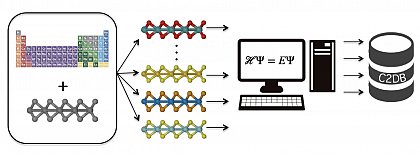
Conceptual sketch of the 2D Material Database. Starting from elementary PSE combinations prototypical lattices are decorated and checked for stability. If stable, various material properties are automatically calculated based on state-of-the-art DFT. The final results are openly available for the users.

Conceptual sketch of the 2D Material Database. Starting from elementary PSE combinations prototypical lattices are decorated and checked for stability. If stable, various material properties are automatically calculated based on state-of-the-art DFT. The final results are openly available for the users.

2D materials refer to crystalline solids consisting of a single (or rarely a few) layer of atoms. A major expectation is that, given their exceptional electronic and optical properties, 2D materials will replace conventional semiconductors to deliver a new generation of electronics. Therefor the solid state community is constantly on the pursuit of discovering new 2D materials.

The Computational 2D Materials Database (C2DB) organises a variety of structural, thermodynamic, elastic, electronic, magnetic, and optical properties of around 1500 2D materials distributed over more than 30 different crystal structures. Material properties are systematically calculated by state-of-the-art density functional theory following a semi- automated workflow. The C2DB is fully open and can be browsed online (http://c2db.fysik.dtu.dk   ). The C2DB identifies a large number of new potentially synthesisable 2D materials with interesting properties targeting applications within spintronics, (opto-)electronics, and plasmonics. The C2DB offers a comprehensive and easily accessible overview of the rapidly expanding family of 2D materials and forms an ideal platform for computational modeling and design of new 2D materials and van der Waals heterostructures.

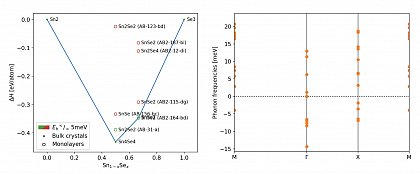
Below an example of cubic 2D SnSe    is given. The material was found to be stable on substrates and interestingly possesses topologically protected metallic edge states, while the bulk remains insulating.

(left) thermodynamical stability of SnSe compounds given by the convex Hull energy (right) dynamical stability indicated by the real/imaginary part of the phonon frequencies at given high symmetry points. While the cubic 2D SnSe (AB-31-a) has a high thermodynamic stability, dynamical instabilities, i.e. soft phonons, can be found. The latter lead to buckling of the free-standing film, but can be stabilised on a substrate.

(left) thermodynamical stability of SnSe compounds given by the convex Hull energy (right) dynamical stability indicated by the real/imaginary part of the phonon frequencies at given high symmetry points. While the cubic 2D SnSe (AB-31-a) has a high thermodynamic stability, dynamical instabilities, i.e. soft phonons, can be found. The latter lead to buckling of the free-standing film, but can be stabilised on a substrate.

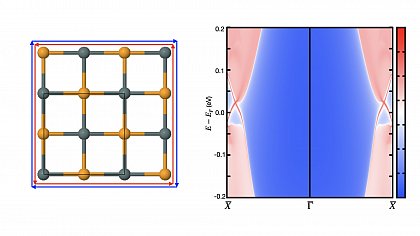
(left) sketch of the atomic structure of cubic 2D SnSe, in a form of monolayer rock salt structure. (right) calculated edge spectral function of SnSe along a high-symmetry line. The intensity of the electronic states is depicted by a color code (red/high, blue/low). Around X at the Fermi energy cross-like states bridge the fundamental band gap and lead to metallic conductance of the material only at the edges. These states are topologically protected against e.g. deformations and impurities.

(left) sketch of the atomic structure of cubic 2D SnSe, in a form of monolayer rock salt structure. (right) calculated edge spectral function of SnSe along a high-symmetry line. The intensity of the electronic states is depicted by a color code (red/high, blue/low). Around X at the Fermi energy cross-like states bridge the fundamental band gap and lead to metallic conductance of the material only at the edges. These states are topologically protected against e.g. deformations and impurities.

Electron-Phonon coupling

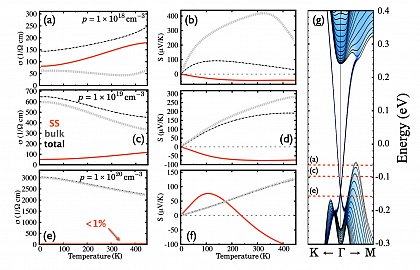
By means of Density Functional Perturbation Theory (DFTP) we are able to calculate the quasiparticle interactions of electrons and phonons (el-ph) as well as phonons and phonons (ph-ph). In particular we’re focusing on the precise evaluation of the collision integral due to the microscopic el-ph and ph-ph interactions from Fermi’s golden rule, which then determines the lifetimes of the quasiparticles. The lifetimes and derived quantities are essential to describe phonon-limited transport properties, e.g. the electronic conductivity or the lattice thermal conductivity. A further benefit is the capability to analyze the impact of phonons, i.e. simply said temperature, onto the renormalization of the bandstructure within the diffusive limit.

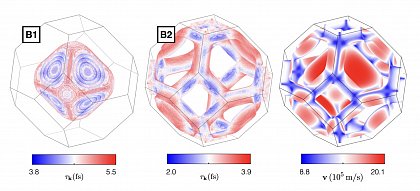
Fermi surfaces of fcc Pb. Shown are the anisotropic state-dependent electron-phonon life times for two contributing bands at the Fermi energy (B1,B2). Additionally given is the Fermi velocity of each state. The larger the lifetime, the smaller is the interaction of an electronic state with all available phonons.

Fermi surfaces of fcc Pb. Shown are the anisotropic state-dependent electron-phonon life times for two contributing bands at the Fermi energy (B1,B2). Additionally given is the Fermi velocity of each state. The larger the lifetime, the smaller is the interaction of an electronic state with all available phonons.

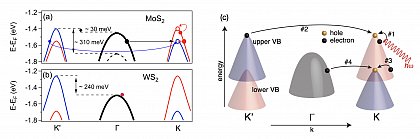
(left) sketch of the valence band structure of 2D MoS2 (a) and 2D WS2 (b, c) for spin-up (red), spin-down (blue) and spin-degenerated states (black). While in MoS2 the band alignments allow for a various amount of electronic scattering mediated by phonons, it is almost forbidden by phase-space requirements in WS2. This leads to a smaller lifetime-broadening and a heavily reduced electronic carrier relaxation once the spin- dependent valleys are occupied.

(left) sketch of the valence band structure of 2D MoS2 (a) and 2D WS2 (b, c) for spin-up (red), spin-down (blue) and spin-degenerated states (black). While in MoS2 the band alignments allow for a various amount of electronic scattering mediated by phonons, it is almost forbidden by phase-space requirements in WS2. This leads to a smaller lifetime-broadening and a heavily reduced electronic carrier relaxation once the spin- dependent valleys are occupied.

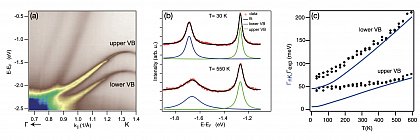
(a) Photoemission intensity of the spin-split valence bands of monolayer WS2 at 30K (b) extracted linewidths from (a) at different temperatures. It can be seen, that the upper valence band states are way less broadened due to reduced electron-phonon interaction. (c) comparison of ab initio theoretical results (blue lines) and photoemission measurements (black dots) of the lifetime broadening of valence band states in monolayer WS2. The interaction with the Au substrate was included.

(a) Photoemission intensity of the spin-split valence bands of monolayer WS2 at 30K (b) extracted linewidths from (a) at different temperatures. It can be seen, that the upper valence band states are way less broadened due to reduced electron-phonon interaction. (c) comparison of ab initio theoretical results (blue lines) and photoemission measurements (black dots) of the lifetime broadening of valence band states in monolayer WS2. The interaction with the Au substrate was included.

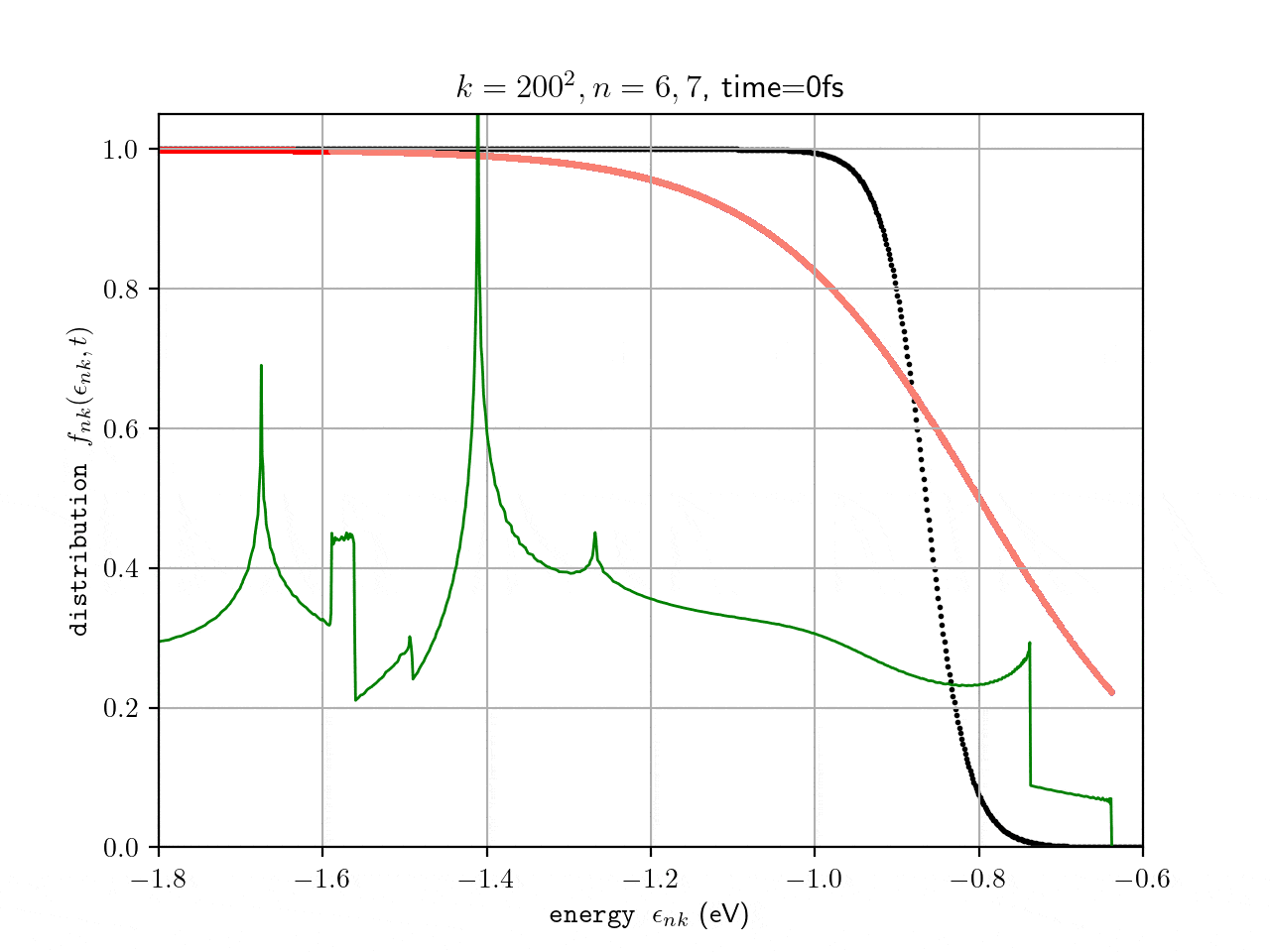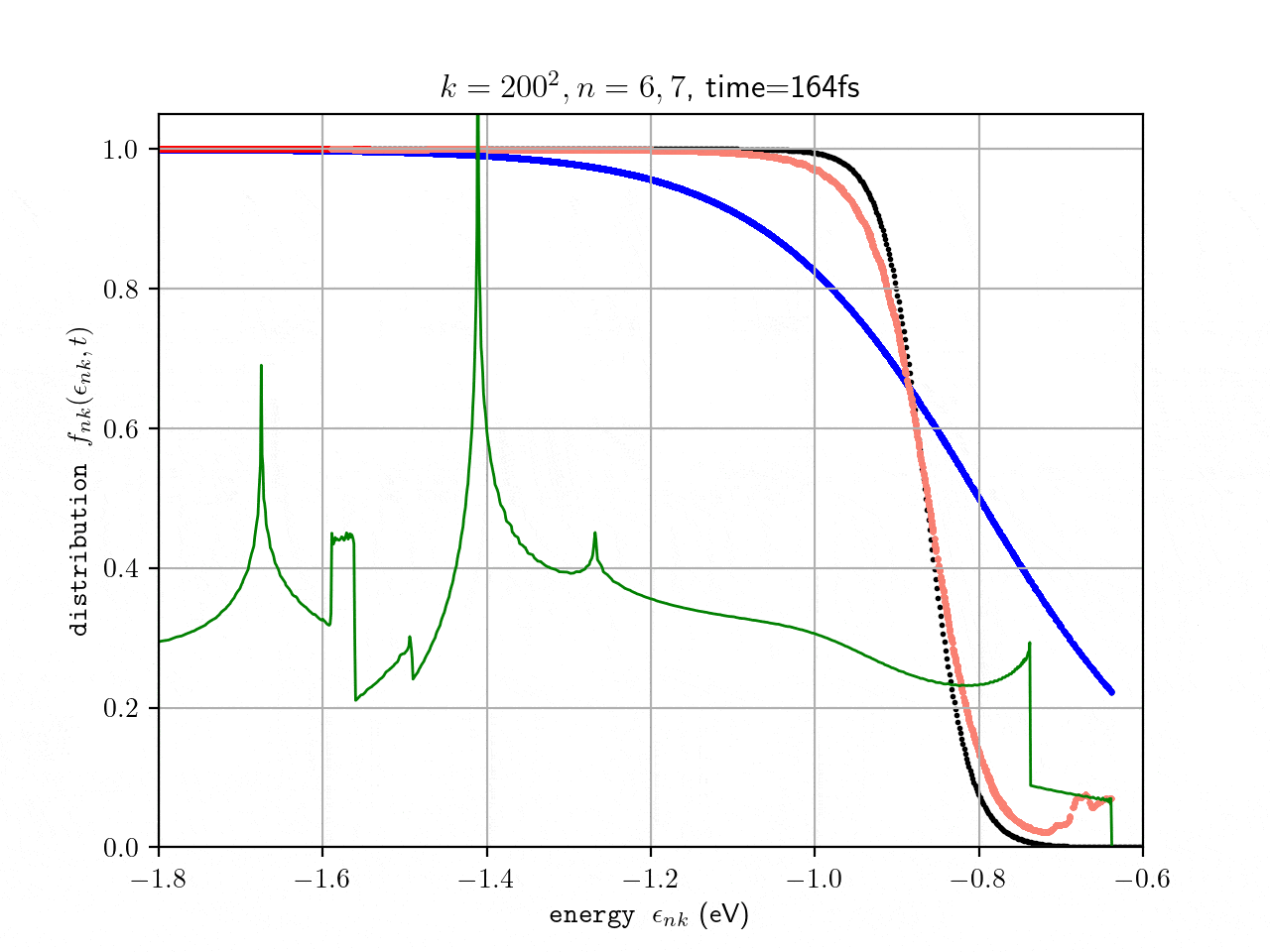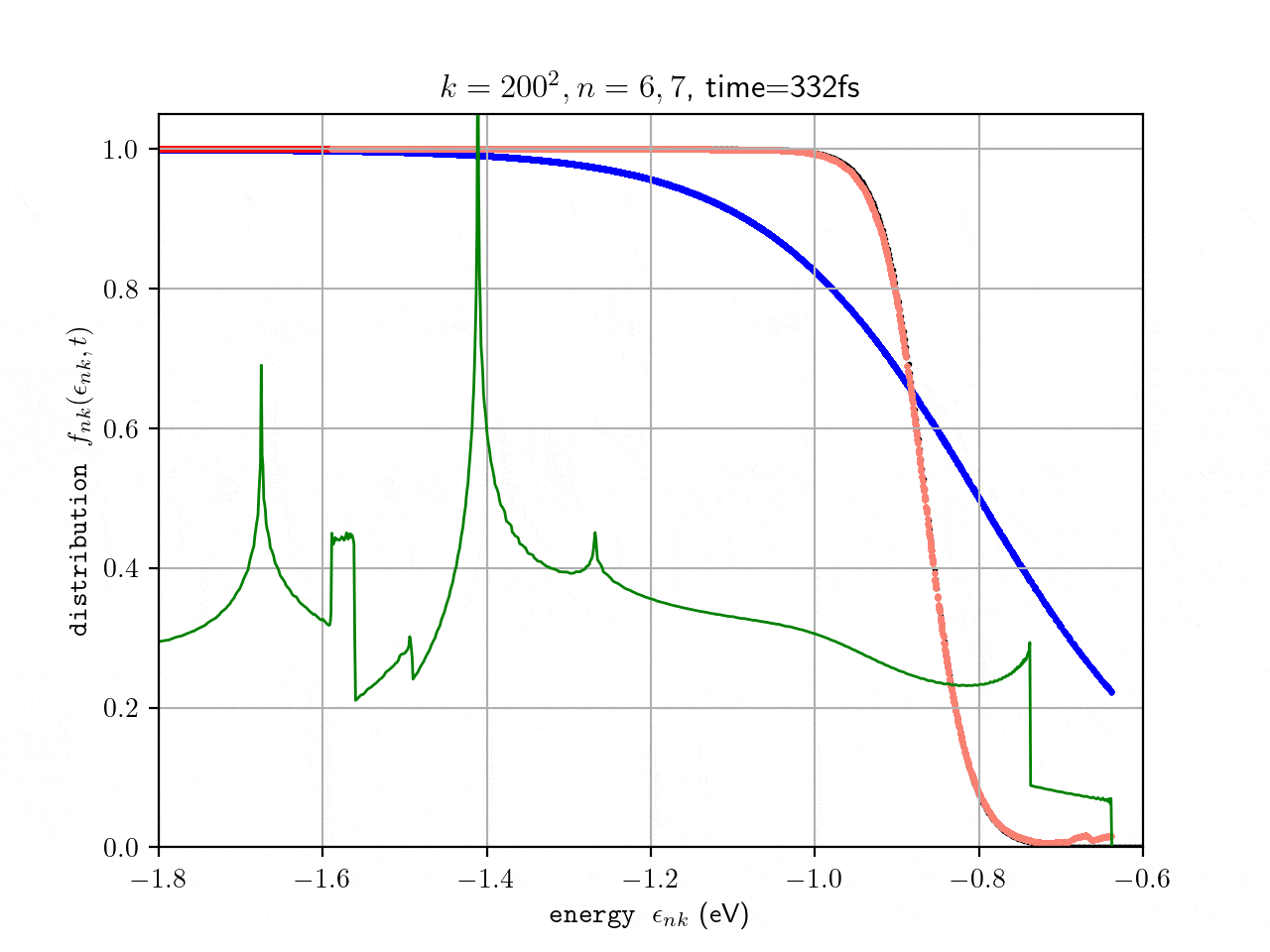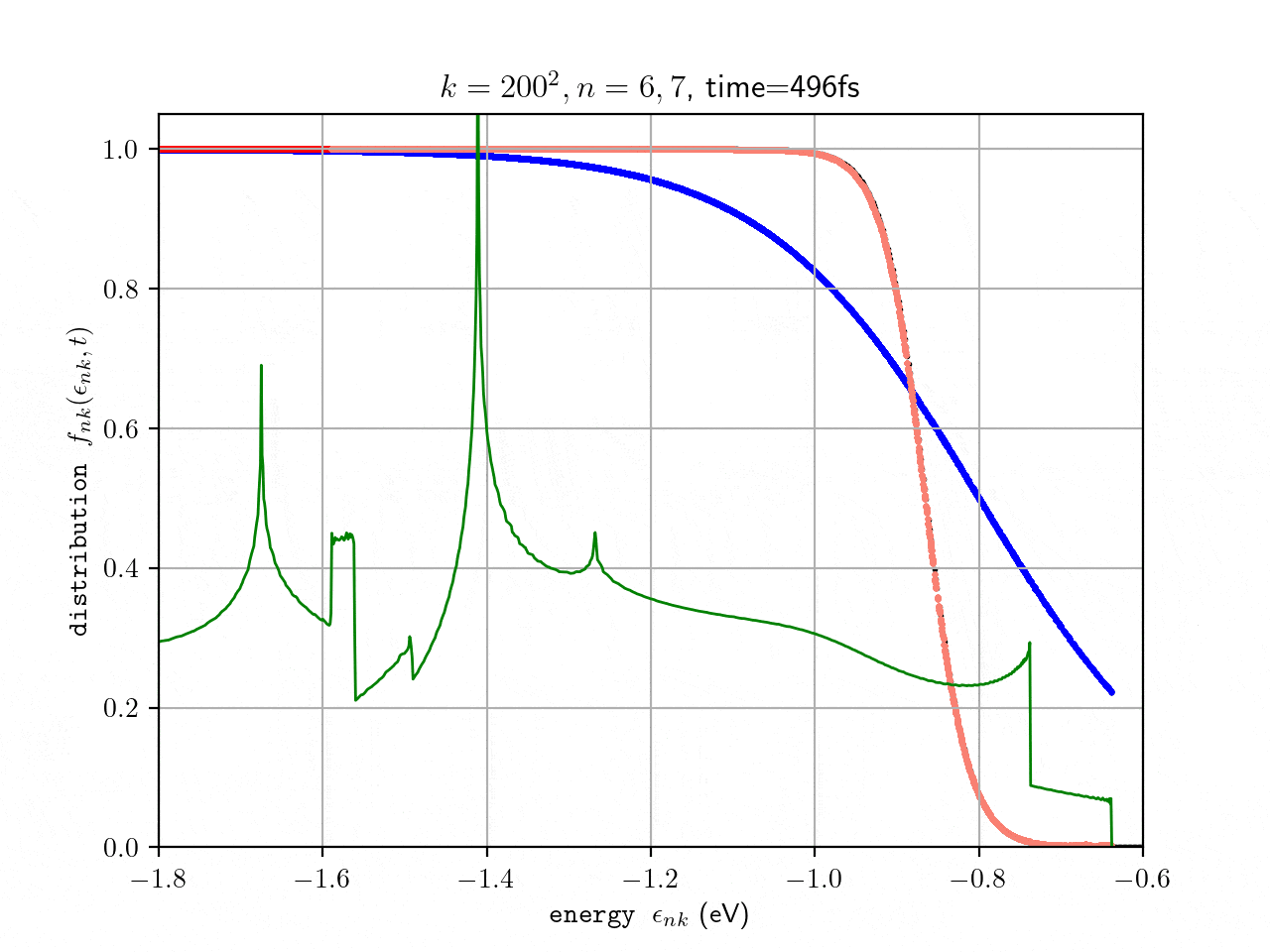
Ultrafast carrier dynamics

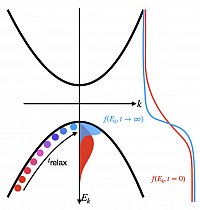
Sketch of semi-conductor bands with an initial thermal excitation of the valence band states (red, high temperature) at t=0. Interactions with phonons allow the electronic carrier distribution f to relax to equilibrium (blue, low temperature). The time scale of the relaxation process is entirely given by the lifetimes (inverse linewidths) linked to the quasiparticle interactions.

Sketch of semi-conductor bands with an initial thermal excitation of the valence band states (red, high temperature) at t=0. Interactions with phonons allow the electronic carrier distribution f to relax to equilibrium (blue, low temperature). The time scale of the relaxation process is entirely given by the lifetimes (inverse linewidths) linked to the quasiparticle interactions.

On basis of ab initio derived electron-phonon (el-ph) and phonon-phonon (ph-ph) quasiparticle interactions the time-dependent Boltzmann Transport Equation (tBTE) can be evaluated to describe ultrafast carrier relaxation processes within the first 100s-1000s fs after excitation. Within Bloch’s Assumption the el-ph and ph-ph tBTE can be decoupled, assuming the phonon system to remain in equilibrium. This approximation already yields very good results on the time-dependent electronic state distribution shortly after thermal or optical excitation. By coupling el-ph and ph-ph tBTE more delicate processes, e.g. the phonon-drag effect, can be calculated at the cost of an elevated computational effort. A theoretical introduction can be e.g. found in Rittweger (2018)   .

Ultrafafast carrier relaxation of thermally excited valence band electrons in MoS2 (here wo SOC) - the initial temperature of the distribution function is set to 1500K (blue), the final temperature to 300K (black). The calculated time- dependent ab initio carrier distribution is given in red. For comparison the density of states is shown in green. The energetically isolated valence bands starts at around E=-0.65eV. Further states contributing to scattering events start at around E=-0.72eV. The dynamics nicely show that most states relax to equilibrium within approximately 200fs, while the states close to the band edge relax significantly slower due to reduced scattering with phonons.

Ultrafafast carrier relaxation of thermally excited valence band electrons in MoS2 (here wo SOC) - the initial temperature of the distribution function is set to 1500K (blue), the final temperature to 300K (black). The calculated time- dependent ab initio carrier distribution is given in red. For comparison the density of states is shown in green. The energetically isolated valence bands starts at around E=-0.65eV. Further states contributing to scattering events start at around E=-0.72eV. The dynamics nicely show that most states relax to equilibrium within approximately 200fs, while the states close to the band edge relax significantly slower due to reduced scattering with phonons.

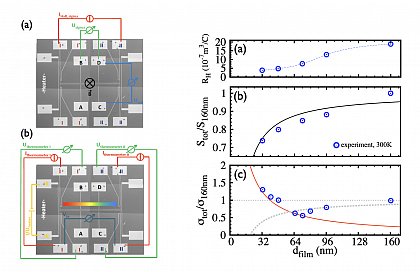
Thermoelectric transport

The research focus lies in understanding the microscopic origin of thermoelectric transport in semiconducting bulk materials, as well as their heterostructures including surface and interface effects.We identify and elucidate mechanisms which could lead to enhanced thermoelectric conversion efficiency. Based on first-principles calculations the electronic structure is determined and lays the foundation to extract the thermoelectric transport properties based on the solution of linearised Boltzmann equations.

Our conceptional ideas were awarded with the „Hugo Junkers Prize“ 2015 for „Most innovative proposal in fundamental research“ (https://www.hugo-junkers-preis.de   ), where we conceptionally showed the bottom-up design of a nanostructured, thermoelectric energy harvester, from theoretical DFT calculations towards the working device.

Introductions into our methods from a classical macroscopic thermodynamical or a more advanced quantum-mechanical microscopical ansatz can be found in

(left, a, b) lithographically defined measurement device to determine the thermoelectric transport properties of thin films. (right, a-c) Experimental and theoretical results for the thermoelectric transport of Sb2Te3 thin films of various thickness. A crossover between a surface-state-dominant (red line) and a Fuchs-Sondheimer (gray dashed line) transport regime is found at around 64nm film thickness.

(left, a, b) lithographically defined measurement device to determine the thermoelectric transport properties of thin films. (right, a-c) Experimental and theoretical results for the thermoelectric transport of Sb2Te3 thin films of various thickness. A crossover between a surface-state-dominant (red line) and a Fuchs-Sondheimer (gray dashed line) transport regime is found at around 64nm film thickness.

(a-f) Thermoelectric transport properties for a 18nm thick Sb2Te3 film at different hole carrier concentrations. The contributions of the bulk states (gray) and the topological surface states (red) are separated by a projection technique. Within and close to the fundamental band gap the surface state (a-d) dictates the behaviour of the thermoelectric transport. (g) Electronic bandstructure around the fundamental bandgap. Red dashed lines indicate the position of the chemical potentials for the three charge carrier concentrations. The topological surface state bridges the fundamental band gap.

(a-f) Thermoelectric transport properties for a 18nm thick Sb2Te3 film at different hole carrier concentrations. The contributions of the bulk states (gray) and the topological surface states (red) are separated by a projection technique. Within and close to the fundamental band gap the surface state (a-d) dictates the behaviour of the thermoelectric transport. (g) Electronic bandstructure around the fundamental bandgap. Red dashed lines indicate the position of the chemical potentials for the three charge carrier concentrations. The topological surface state bridges the fundamental band gap.

Zum Seitenanfang